Say you have an array for which the $i^{th}$ element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Example 1:

1
2
3
4
Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
             Not 7-1 = 6, as selling price needs to be larger than buying price.

Example 2:

1
2
3
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

题目要求为，选择最佳的买入卖出时间，得到最大收益。

暴力搜索

复杂度$O(n^2)$ 确切一点是 $O(\frac{n(n+1)}{2})$

one pass

对于$[7, 1, 5, 3, 6, 4] $

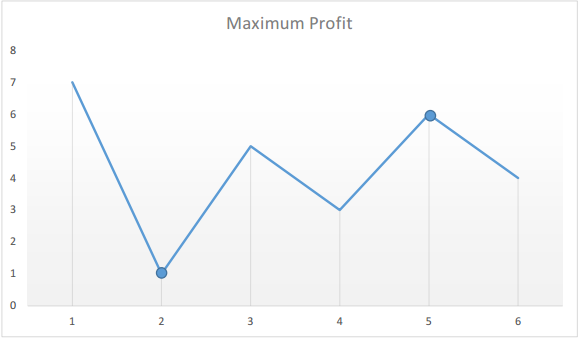
Profit Graph

可以知道，我们感兴趣的是峰谷之间的差值。则我们只需要找到当前值与之前最小值的最大差值即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
public class Solution {
    public int maxProfit(int prices[]) {
        int minprice = Integer.MAX_VALUE;
        int maxprofit = 0;
        for (int i = 0; i < prices.length; i++) {
            if (prices[i] < minprice)
                minprice = prices[i];
            else if (prices[i] - minprice > maxprofit)
                maxprofit = prices[i] - minprice;
        }
        return maxprofit;
    }
}