描述

n阶楼梯，每次一步或者两步，一共有多少种方法

[Solutions](../prob_70_Climbing Stairs.py)

brute_force

$f(n)=f(n-1)+f(n-2)$

显然有，到第n阶楼梯有两种方法，从n-1过去，和n-2过去。即到n阶的方法等于这两种方法的和

1
2
3
4
def brute_force(n):
    if n == 1 or n == 2:
        return n
    return brute_force(n-1)+brute_force(n-2)

这种方法的时间复杂度为 $2^n$. 图片来自于leetcode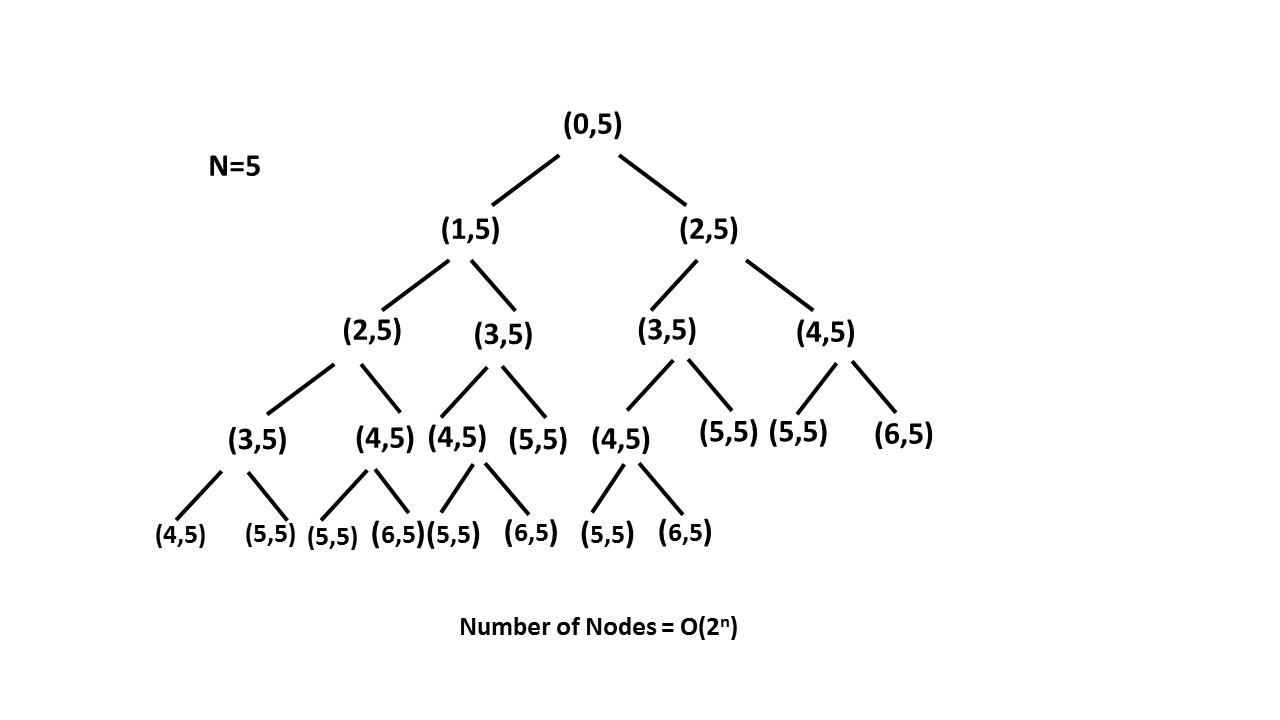Climbing_Stairs

带记忆的递归计算

在上面的计算中，显然有大量的重复计算，如果这个数值已经存下来了，就可以减小运算时间

1
2
3
4
5
6
7
8
9
memo = {}
def recursion_memo(n, memo):
    if n==1 or n ==2:
        return n
    if n in memo.keys():
        return memo[n]
    value = recursion_memo(n-1, memo) + recursion_memo(n-2, memo)
    memo.update({n:value})
    return memo[n]

动态规划

在暴力搜索里提到了，$f(n)=f(n-1)+f(n-2)$

1
2
3
4
5
6
7
8
9
10
def dynamic(n):
    if n == 1 or n == 2:
        return n
    result = [0]*(n)
    result[0] =1
    result[1] =2
    for i in range(2, n):
        result[i] = result[i-1]+result[i-2]
    return result[n-1]